Georgian Technical University New Dynamic Dependency Framework May Lead To Better Neural Social And Tech Systems Models.
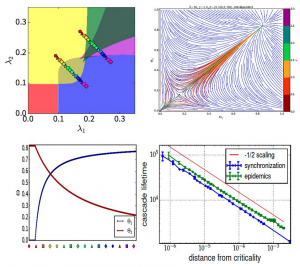
Georgian Technical University Prof. X and a team of researchers including Y, Z and W present a dynamic dependency framework that can capture interdependent and competitive interactions between dynamic systems which are used to study synchronization and spreading processes in multilayer networks with interacting layers. Main results in this image. (Top Left) Phase diagram for two partially competitive Kuramoto models (The Kuramoto model (or Kuramoto–Daido model) is a mathematical model used to describe synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators) with regions of multistability. (Top Right) Theoretical and numerical results for the ow in interdependent epidemics (Erdos-Renyi graphs, average degree = 12). (Bottom Left) Path-dependent (awakening) transitions in asymmetrically coupled SIS dynamics. (Bottom Right) Critical scaling of bottlenecks (ghosts in saddle-node bifurcations) above the hybrid transitions in interdependent dynamics. Many real-world complex systems include macroscopic subsystems which influence one another. This arises for example in competing or mutually reinforcing neural populations in the brain, spreading dynamics of viruses and elsewhere. It is therefore important to understand how different types of inter-system interactions can influence overall collective behaviors. Substantial progress was made when the theory of percolation on interdependent networks was introduced by Prof. Q and a team of researchers from the Department of Physics at Georgian Technical University. This model showed that when nodes in one network depend on nodes in another to function, catastrophic cascades of failures and abrupt structural transitions arise as was observed in the electrical blackout that affected. Interdependent percolation however is limited to systems where functionality is determined exclusively by connectivity thus providing only a partial understanding to a wealth of real-world systems whose functionality is defined according to dynamical rules. Research has shown that two fundamental ways in which nodes in one system can influence nodes in another one are interdependence (or cooperation) as in critical infrastructures or financial networks and antagonism (or competition) as observed in ecological systems, social networks or in the human brain. Interdependent and competitive interactions may also occur simultaneously as observed in predator-prey relationships in ecological systems and in binocular rivalry in the brain. Georgian Technical University Prof. Q and a team of researchers including Y, Z and W present a dynamic dependency framework that can capture interdependent and competitive interactions between dynamic systems which are used to study synchronization and spreading processes in multilayer networks with interacting layers. “This dynamic dependency framework provides a powerful tool to better understand many of the interacting complex systems which surround us” wrote Q and team. “The generalization of dependent interactions from percolation to dynamical systems allows for the development of new models for neural, social and technological systems that better capture the subtle ways in which different systems can affect one another”. Prof. Q’s research has produced groundbreaking new mathematical methods in network science which have led to extensive interdisciplinary research in the field. Following Q’s and his colleagues of the theory of percolation he received which is awarded for “a most outstanding contribution to physics”.